Difference between revisions of "VT2021 Merkle Trees fiche"
| Line 19: | Line 19: | ||
Les arbres de Merkle sont des structure de données organisées en arbres (binaires en général) utilisées pour effectuer de la vérification de données sur Internet. Chaque noeud de l'arbre va contenir un hachage différent. Le hachage pour un noeud est obtenu en concaténant le hashage de ses deux enfants et en passant le résultat dans une fonction de hashage. Il se construit donc une dépendance général ou la valeur de chaque noeud dépend de ses noeuds enfants. Les feuilles de l'arbre vont contenir le hachage correspondant aux données que l'on cherche à valider. |
Les arbres de Merkle sont des structure de données organisées en arbres (binaires en général) utilisées pour effectuer de la vérification de données sur Internet. Chaque noeud de l'arbre va contenir un hachage différent. Le hachage pour un noeud est obtenu en concaténant le hashage de ses deux enfants et en passant le résultat dans une fonction de hashage. Il se construit donc une dépendance général ou la valeur de chaque noeud dépend de ses noeuds enfants. Les feuilles de l'arbre vont contenir le hachage correspondant aux données que l'on cherche à valider. |
||
| + | |||
| + | [[File:Merkle_Tree.png]] |
||
=== Un point sur le hachage === |
=== Un point sur le hachage === |
||
Revision as of 17:24, 2 December 2021
Présenté par :
- Corentin Humbert : corentin.humbert@etu.univ-grenoble-alpes.fr
- Kévin Yung : kevin.yung@etu.univ-grenoble-alpes.fr
Merkle Trees
Résumé
Mots-clé: Merkle, arbres, hachage, structure de données, validation
Abstract
Merkle Trees are binary trees in which every node is labelled with a cryptographic hash.
Keywords: Merkle, Trees, hash, data structure, validation
Fonctionnement
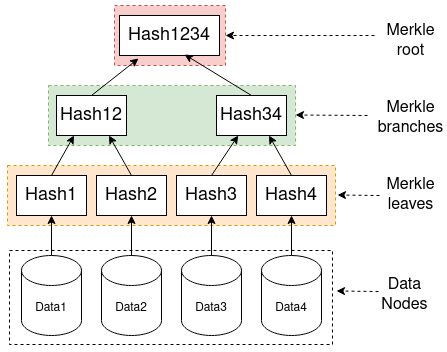
Les arbres de Merkle sont des structure de données organisées en arbres (binaires en général) utilisées pour effectuer de la vérification de données sur Internet. Chaque noeud de l'arbre va contenir un hachage différent. Le hachage pour un noeud est obtenu en concaténant le hashage de ses deux enfants et en passant le résultat dans une fonction de hashage. Il se construit donc une dépendance général ou la valeur de chaque noeud dépend de ses noeuds enfants. Les feuilles de l'arbre vont contenir le hachage correspondant aux données que l'on cherche à valider.
Un point sur le hachage
En cryptographie, une fonction de hachage est une fonction qui, à partir d'une donnée fournie en entrée, va être capable de calculer une empreinte numérique qui va permettre d'identifier rapidement la donnée initiale. Ce qui fait la puissance et la fiabilité d'une fonction de hachage c'est l'incapacité de remonter à la donnée initiale à partir de son empreinte. Il est donc pour une donnée en entrée, très simple de calculer son hachage, alors qu'il est mathématiquement extrêmement compliqué de remonter d'un hachage à la donnée source. Une utilisation notable du hachage de nos jours va être pour le stockage de mots de passe. Lors d'une inscription sur un site Web, on ne va directement stocker le mot de passe en clair dans une base de données. A la place, on va calculer le hachage du mot de passe et c'est cela que l'on va stocker dans la base. A chaque fois que l'on voudra s'authentifier sur le dit site en rentrant le mot de passe, le hachage sera calculé et comparé à celui présent dans la base de données. Si les deux sont égaux, alors il s'agit du bon mot de passe. On peut donc vérifier qu'un mot de passe est valide sans l'avoir stocker dans la base au préalable, ce qui sécurise d'avantage les comptes utilisateurs.
Toutefois, les fonctions de hachage ne sont pas parfaites, certains algorithmes ont été rendu obsolète pour l'utilisation sécurisée du hachage tel que MD5. Il est fortement déconseillé de stocker des hachages MD5 de mots de passe étant donné qu'avec la puissance dont nos ordinateurs disposent aujourd'hui, l'opération permettant de retrouver le mot de passe à partir de son empreinte est facilement exécutable. On privilégiera donc des fonctions de hachage plus sécurisées comme SHA2, SHA-256 ou encore SHA3.
<img merkle tree>
Création d'un arbre
Pour réaliser un arbre de Merkle pour une donnée particulière, on va commencer par découper la donnée en entrée en un certain nombres de blocs. Le nombre de blocs va varier en fonction de la taille de la donnée. Une fois la donnée scindée en blocs, on va calculer pour chaque bloc son hachage et l'ajouter à l'arbre de Merkle. Deux blocs consécutifs vont être reliés par un nouveau noeud parent dont le hachage sera calculé en effectuant la concaténation des deux hachages enfant et en hachant une dernière fois ce résultat. On va réitérer cette opération pour chaque bloc, jusqu'à ce que tous les blocs de données hachés appartiennent à l'abre et qu'une racine soit calculée. Une fois la racine obtenue, la construction de l'abre est terminée.
Pour ce qui est de l'algorithme de hachage utilisé, celui-ci va varier en fonction des implémentations. Généralement, on utilisera des fonctions de hachage robustes tel que le SHA2 ou SHA3.
Arbre de Merkle désiquilibré
Nous avons parlé précédemment de comment les abres de Merkel étaient construits mais nous avons oublié d'évoquer un point. L'algorithme décrit marche très bien lorsque le nombre de blocs en entrée est une puissance de 2. Par exemple, avec quatre blocs, on aura quatre feuilles (noeud de hauteur 2), deux noeuds de hauteur 1 et un noeud de hauteur 0 (la racine). Mais que se passe-t-il si au lieu d'avoir quatre blocs, nous en avions six ? Nous aurions alors six feuilles, trois noeuds de hauteur 1 et... Comment faire? Chaque noeud ne peut avoir que deux enfants et nous nous trouvons avec un nombre impair de noeud, devons-nous changer la structure de l'abre et autoriser des noeuds à avoir trois enfants ?
Ils existent différentes approches permettant de pallier ce problème.
Duplication du noeud impair (Bitcoin)
Pour cette première approche, on va dupliquer les noeuds qui se retrouvent tout seul. Dans l'exemple suivant, on va donc dupliquer Hash5 de manière à pouvoir créer un parent dont les enfants seront deux copies de Hash5. On va réitérer l'opération à chaque fois qu'on montera d'un niveau de manière à avoir un arbre équilibré.