VT2021 Merkle Trees fiche

⚠️ Cette page est en cours de construction et de ce fait beaucoup d'informations sont encore manquantes... ⚠️

Présenté par :

• Corentin Humbert : corentin.humbert@etu.univ-grenoble-alpes.fr
• Kévin Yung : kevin.yung@etu.univ-grenoble-alpes.fr

Merkle Trees

Résumé

Mots-clé: Merkle, arbres, hachage, structure de données, validation

Abstract

Merkle Trees are binary trees in which every node is labelled with a cryptographic hash.

Keywords: Merkle, Trees, hash, data structure, validation

Fonctionnement

Principe

Figure 1 : Exemple d'arbre de Merkle

Les arbres de Merkle sont des arbres binaires utilisés pour effectuer de la validation de données. Pour ce faire, chaque feuille de l'arbre va contenir le hachage correspondant à une partie de la donnée à valider. Chaque nœud de l'arbre va également contenir un hachage. Ce hachage est obtenu en concaténant le hachage des deux enfants et en passant le résultat dans une fonction pour créer un tout nouveau hachage. Il se construit alors une dépendance générale où la valeur de chaque nœud dépend des valeurs de ses nœuds enfants.

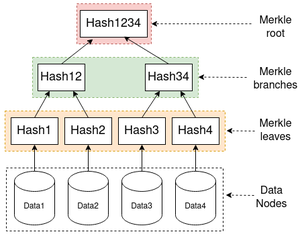
L'image ci-dessous contient un arbre de Merkle servant à valider une donnée découpée en quatre blocs (Data Nodes). Les feuilles de l'abre (Merkle leaves) vont contenir le hachage correspondant pour chaque bloc. Les nœuds intermédiaires (Merkle branches) vont contenir le hachage issu de la concaténation des hachages de leurs deux enfants. Enfin, la racine de l'arbre (Merkle root) va contenir le hachage final servant à identifier l'arbre de Merkle.

Un point sur le hachage

Avant de s'immiscer dans le fonctionnement des arbres, il est important de parler du hachage et plus particulièrement des fonctions de hachage.

Figure 2 : Exemples de hachages obtenus en utilisant MD5 (source: Wikipedia)

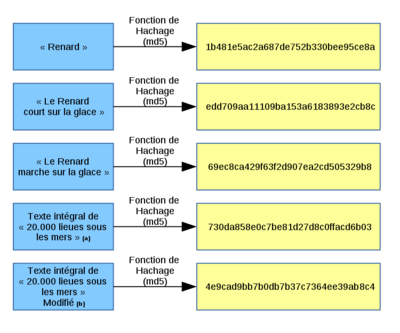
En cryptographie, une fonction de hachage est une fonction qui, à partir d'une donnée fournie en entrée, va être capable de calculer une empreinte numérique permettant d'identifier la donnée initiale de manière unique. La taille en sortie de cette empreinte est fixe et ne dépend pas de la taille de la donnée en entrée. Par idempotence, chaque donnée donnera toujours la même empreinte. En pratique, les fonctions de hachages sont bijectives, dans le sens où chaque donnée a une seule empreinte et chaque empreinte ne correspond qu'à une seule donnée. En théorie, la possibilité de surjectivité existe. Cela est due au fait que l'ensemble d'arrivée correspondant aux empreintes est de taille fini contrairement à l'ensemble des données en entrées qui lui peut être infini. On pourrait donc trouver deux données différentes partageant une même empreinte. Cependant, l'ensemble d'arrivée est en général suffisamment grand pour que ce phénomène ne se produise jamais. On parle souvent de la capacité qu'a une fonction de hachage à résister aux collisions (deux données différentes partageant une même empreinte). Cette capacité à résister aux collisions varie en fonction des algorithmes. Certains algorithmes réduisent d'ailleurs l'ensemble d'entrée en un ensemble fini pour s'assurer que le phénomène de collision ne se produise jamais. La présence de collisions constitue cependant une faille de sécurité importante pour les fonctions de hachages et un problème qu'on ne peut pas ignorer.

Difficilement réversible

Ce qui fait la puissance et la fiabilité d'une fonction de hachage, c'est la difficulté de retrouver la donnée initiale à partir de son empreinte. Il est très simple, pour une donnée en entrée, de calculer le hachage correspondant. Alors que l'opération inverse, qui correspond à retrouver la donnée initiale à partir de l'empreinte est mathématiquement extrêmement compliquée, et impossible à mettre en place sur les ordinateurs de nos jours. Une utilisation notable du hachage va être le stockage de mots de passe. Lors d'une inscription sur un site web, on ne va jamais stocker le mot de passe en clair dans une base de données. À la place, on va calculer le hachage correspondant au mot de passe et le stocker dans la base. À chaque fois que l'on voudra s'authentifier sur le site en rentrant le mot de passe, le hachage sera calculé et comparé à celui présent dans la base de données. Si les deux sont égaux, alors il s'agit du bon mot de passe. On peut donc vérifier qu'un mot de passe est valide sans l'avoir stocké dans la base au préalable, ce qui sécurise davantage les comptes utilisateurs.

Résistance aux collisions

Les fonctions de hachage ont tout de même quelques faiblesses notables. La première, réside dans la complexité de l'algorithme de hachage et de sa résistance aux collisions. C'est le cas de la fonction MD5 inventée en 1991 par Ronald Rivest, qui a pu être utilisée de manière fiable jusqu'en 2004 où une équipe chinoise a réussi à casser la fonction et prouver qu'elle ne garantissait une assez bonne résistance aux collisions. Le MD5 est aujourd'hui encore utilisé dans certains cas de figure. (notamment pour vérifier l'intégrité d'une donnée, c'est le cas pour les sommes de contrôle de certaines distributions Linux par exemple.) Toutefois, il est à bannir pour le hachage de mots de passe qui sont des données extrêmement sensibles. Il existe aujourd'hui des fonctions de hachage sécurisées telles que les fonctions dites SHA (pour Secure Hashing Algorithm) et plus précisément les familles de fonctions SHA-2 et SHA-3 qui n'ont pas encore été cassées.

Limites du hachage

Une autre faiblesse des fonctions de hachage est l'idempotence. Puisque chaque donnée a une empreinte unique, un attaquant pourrait calculer en amont les hachages pour des centaines de millions de données différentes et se contenter de les comparer à des hachages volés dans des bases de données de manière à identifier la donnée source. Dans le cadre du vol de mot de passe, on parle de rainbow table qui sont simplement des gigantesques tables faisant correspondre un mot de passe à son hachage. Il existe différentes méthodes que l'on peut mettre en place pour limiter le vol de mots de passe tel que le principe de salage ou encore l'utilisation d'algorithmes lents, comme bcrypt visant à ralentir l'opération de hachage.

Enfin, il est important de garder à l'esprit que toutes les méthodes mises en place ne résolvent pas le problème, elles visent simplement à ralentir considérablement les attaquants. Un attaquant disposant de suffisamment de temps et de puissance de calcul finira par retrouver n'importe quel mot de passe. Il y a également les récentes innovations au niveau des ordinateurs quantiques qui sont vouées à compromettre significativement les dispositifs de sécurité mis en place sur Internet aujourd'hui. Nous ne nous étendrons pas plus sur le sujet du hachage dans ce document, si vous désirez en apprendre davantage, je vous invite à cliquer sur les différents liens hypertextes présents dans cette partie.

Création d'un arbre

Pour réaliser un arbre de Merkle pour une donnée particulière, on va commencer par découper la donnée en entrée en un certain nombres de blocs. Le nombre de blocs va varier en fonction de la taille de la donnée. Une fois la donnée scindée en blocs, on va calculer pour chaque bloc son hachage et l'ajouter à l'arbre de Merkle. Deux blocs consécutifs vont être reliés par un nouveau nœud parent dont le hachage sera calculé en effectuant la concaténation des deux hachages enfant et en hachant une dernière fois ce résultat. On va réitérer cette opération pour chaque bloc, jusqu'à ce que tous les blocs de données hachés appartiennent à l'abre et qu'une racine soit calculée. Une fois la racine obtenue, la construction de l'abre est terminée.

Pour ce qui est de l'algorithme de hachage utilisé, celui-ci va varier en fonction des implémentations. Généralement, on utilisera des fonctions de hachage robustes tel que le SHA2 ou SHA3.

Arbre de Merkle désiquilibré

Nous avons parlé précédemment de comment les abres de Merkel étaient construits mais nous avons oublié d'évoquer un point. L'algorithme décrit marche très bien lorsque le nombre de blocs en entrée est une puissance de 2. Par exemple, avec quatre blocs, on aura quatre feuilles (nœud de hauteur 2), deux nœuds de hauteur 1 et un nœud de hauteur 0 (la racine). Mais que se passe-t-il si au lieu d'avoir quatre blocs, nous en avions six ? Nous aurions alors six feuilles, trois nœuds de hauteur 1 et... Comment faire? Chaque nœud ne peut avoir que deux enfants et nous nous trouvons avec un nombre impair de nœud, devons-nous changer la structure de l'abre et autoriser des nœuds à avoir trois enfants ?

Ils existent différentes approches permettant de pallier ce problème.

Duplication du nœud impair (Bitcoin)

Figure 3 : Équilibrage d'un abre de Merkle en utilisant la technique de duplication (source: Medium)

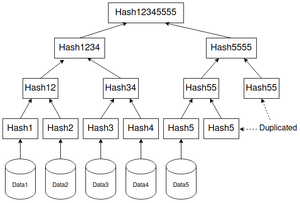
Pour cette première approche, on va dupliquer les nœuds qui se retrouvent tout seul. Sur la figure 3, on peut observer que l'arbre de Merkle contient cinq feuilles. Cinq étant un chiffre impair, notre arbre de Merkle se retrouve déséquilibré. On va donc choisir de dupliquer la feuille se retrouvant toute seule pour ré-équilibrer l'arbre. Ici, il va s'agir de la feuille contenant le hachage du cinquième bloc de donnée : Hash5. La feuille va donc être copiée de manière à faire apparaître une sixième feuille contenant également Hash5. Il n'y a plus de problème au niveau des feuilles de l'arbre puisqu'il y en a désormais une quantité paire. Cependant, nous allons rencontrer un problème au niveau supérieur. En effet, nos six feuilles vont se transformer en trois nœuds et on retombe encore une fois sur une quantité impaire. On va donc ré-itérer le procédé et dupliquer cette fois le troisième nœud contenant Hash55 (On remarque que ce hachage est obtenu en appliquant la fonction de hachage sur la concaténation de deux hachages identiques.). Cela nous permet de faire un quatrième nœud, le nombre de nœuds du niveau étant paire, on peut passer au niveau suivant. Pour l'avant dernier niveau, on va avoir deux fois moins de nœuds que le niveau précédent, ce qui nous ramène à deux nœuds. Comme la quantité de nœuds est paire, pas besoin de dupliquer de nœud. L'algorithme de duplication prend fin ici puisque le prochain niveau va simplement contenir la racine.

Notre arbre de Merkle est donc désormais équilibré et exploitable. On pourrait cependant se poser des questions sur la fiabilité de cette solution de duplication. En effet, celle-ci est assez simple à mettre en place, mais il introduit une faille de sécurité notable car certains nœuds ne contiendront en réalité qu'un seul hachage. (copié deux fois)

Création d'un arbre parfait (Monero)

Figure 4 : Équilibrage d'un abre de Merkle en utilisant la technique de création d'arbre parfait (source: Medium)

Cette seconde méthode va consister à transformer n'importe quel arbre déséquilibré en un arbre parfait dès la première itération. En d'autres termes, quelque soit le nombre de blocs de données en entrée, on aura un arbre équilibré dès le premier niveau de branches (juste au dessus des feuilles). La différence avec la précédente approche où l'on duplicait les nœuds impairs et les fusionnait avec eux-même est notable puisqu'ici on ne va pas avoir à vérifier la parité du nombre de nœuds à chaque niveau mais seulement au tout début. L'idée va donc être de pré-calculer le nombre de transformations nécessaires sur les feuilles pour que l'on obtienne une quantité de nœuds au niveau suivant les feuilles qui soit une puissance de deux.

L'algorithme utilisé est le suivant :

• On commence par trouver x, tel que 2^x soit supérieur au nombre de blocs de données. (cela revient à utiliser un logarithme en base 2)
• On soustrait ensuite à 2^x le nombre de blocs de données, cela va nous donner l'indice auquel nous allons commencer la première itération de construction de l'arbre
• On procède en effectuant la première itération à partir du bloc de donnée correspondant à l'indice trouvé.
• Une fois la première itération terminée, le nombre de nœuds à l'itération suivante est une puissance de deux, on peut procéder normalement sans avoir à se soucier de potentiels problème de parité.

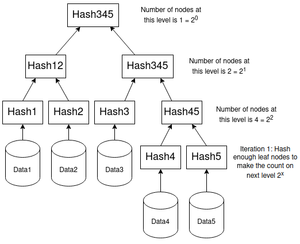
Pour nous aider à visualiser le fonctionnement de cette approche, nous allons travailler avec l'exemple de la figure 4. Au premier coup d'œil on remarque que l'abre a une structure un peu bizarre; on a deux niveaux de feuilles. Executons l'algorithme sans attendre pour comprendre ce qu'il se passe :

• On dispose de cinq blocs de données (Data1 jusqu'à Data5). Si on cherche x tel que 2^x > 5, on trouve 2^3 = 8 > 4, soit x = 3.
• On soustrait désormais le nombre de blocs à la puissance trouvée, soit 8 - 5 = 3, ce qui nous donne l'indice de départ pour la première itération. On commencant à compter les indices à partir de zéro, l'indice 3 va correspondre à Data4. Tous les blocs qui suivent Data4, lui y compris vont participer à la première itération. Tandis que tous ceux qui le précède vont attendre l'itération d'après.
• On lance la première itération qui ne concerne ici que Data4 et Data5. On va donc naturellement calculer leur hachage respectif, ce qui nous donne Hash4 et Hash5, que l'on va concaténer et hacher de manière à obtenir Hash45, qui lui, appartient à la seconde itération. La première itération est désormais terminée puisque Data5 était le dernier nœud.
• On commence la seconde itération, avec cette fois non pas cinq nœuds mais quatre: Hash1, Hash2, Hash3 et le hachage Hash45 obtenu lors de l'itération précédente. Comme le nombre de nœuds est une puissance de deux, rien de plus simple, on va concaténer Hash1 et Hash2 pour obtenir Hash12, et Hash3 et Hash45 pour obtenir Hash345. La seoncde itération se termine. La dernière itération va concaténer Hash12 et Hash345, ce qui va nous permettre d'obtenir Hash12345.

Références

• "Merkle tree", Wikipedia, https://en.wikipedia.org/wiki/Merkle_tree
• "Merkle Trees: Concepts and Use Cases", Medium, https://medium.com/coinmonks/merkle-trees-concepts-and-use-cases-5da873702318