VT2021 Merkle Trees fiche: Difference between revisions
mNo edit summary |
No edit summary |
||
| Line 68: | Line 68: | ||
=== Création d'un arbre === |
=== Création d'un arbre === |
||
Pour réaliser un arbre de Merkle pour une donnée particulière, on va commencer par découper la donnée en entrée en un certain nombres de blocs. Le nombre de blocs va varier en fonction de la taille de la donnée. Une fois la donnée scindée en blocs, on va calculer pour chaque bloc son hachage et l'ajouter à l'arbre de Merkle. Deux blocs consécutifs vont être reliés par un nouveau nœud parent dont le hachage sera calculé en effectuant la concaténation des deux hachages enfant et en hachant une dernière fois ce résultat. On va réitérer cette opération pour chaque bloc, jusqu'à ce que tous les blocs de données hachés appartiennent à l' |
Pour réaliser un arbre de Merkle pour une donnée particulière, on va commencer par découper la donnée en entrée en un certain nombres de blocs. Le nombre de blocs va varier en fonction de la taille de la donnée. Une fois la donnée scindée en blocs, on va calculer pour chaque bloc son hachage et l'ajouter à l'arbre de Merkle. Deux blocs consécutifs vont être reliés par un nouveau nœud parent dont le hachage sera calculé en effectuant la concaténation des deux hachages enfant et en hachant une dernière fois ce résultat. On va réitérer cette opération pour chaque bloc, jusqu'à ce que tous les blocs de données hachés appartiennent à l'arbre et qu'une racine soit calculée. Une fois la racine obtenue, la construction de l'arbre est terminée. |
||
Pour ce qui est de l'algorithme de hachage utilisé, celui-ci va varier en fonction des implémentations. Généralement, on utilisera des fonctions de hachage robustes tel que le SHA2 ou SHA3. |
Pour ce qui est de l'algorithme de hachage utilisé, celui-ci va varier en fonction des implémentations. Généralement, on utilisera des fonctions de hachage robustes tel que le SHA2 ou SHA3. |
||
| Line 74: | Line 74: | ||
=== Arbre de Merkle déséquilibré === |
=== Arbre de Merkle déséquilibré === |
||
Nous avons parlé précédemment de comment les arbres de Merkel étaient construits mais nous avons oublié d'évoquer un point. L'algorithme décrit marche très bien lorsque le nombre de blocs en entrée est une puissance de 2. Par exemple, avec quatre blocs, on aura quatre feuilles (nœud de hauteur 2), deux nœuds de hauteur 1 et un nœud de hauteur 0 (la racine). Mais que se passe-t-il si au lieu d'avoir quatre blocs, nous en avions six ? Nous aurions alors six feuilles, trois nœuds de hauteur 1 et... |
Nous avons parlé précédemment de comment les arbres de Merkel étaient construits, mais nous avons oublié d'évoquer un point. L'algorithme décrit marche très bien lorsque le nombre de blocs en entrée est une puissance de 2. Par exemple, avec quatre blocs, on aura quatre feuilles (nœud de hauteur 2), deux nœuds de hauteur 1 et un nœud de hauteur 0 (la racine). Mais que se passe-t-il si au lieu d'avoir quatre blocs, nous en avions six ? Nous aurions alors six feuilles, trois nœuds de hauteur 1 et... |
||
Comment faire? Chaque nœud ne peut avoir que deux enfants et nous nous trouvons avec un nombre impair de nœud, devons-nous changer la structure de l'arbre et autoriser des nœuds à avoir trois enfants ? |
Comment faire ? Chaque nœud ne peut avoir que deux enfants et nous nous trouvons avec un nombre impair de nœud, devons-nous changer la structure de l'arbre et autoriser des nœuds à avoir trois enfants ? |
||
Ils existent différentes approches permettant de pallier ce problème. |
Ils existent différentes approches permettant de pallier ce problème. |
||
| Line 83: | Line 83: | ||
[[File:Merkle_Tree_Duplicating_Node.png|thumb|right|'''Figure 3 :''' Équilibrage d'un arbre de Merkle en utilisant la technique de duplication (source: Medium)]] |
[[File:Merkle_Tree_Duplicating_Node.png|thumb|right|'''Figure 3 :''' Équilibrage d'un arbre de Merkle en utilisant la technique de duplication (source: Medium)]] |
||
Pour cette première approche, on va dupliquer les nœuds qui se retrouvent tout seul. Sur la '''figure 3''', on peut observer que l'arbre de Merkle contient cinq feuilles. Cinq étant un chiffre impair, notre arbre de Merkle se retrouve déséquilibré. On va donc choisir de dupliquer la feuille se retrouvant toute seule pour ré-équilibrer l'arbre. Ici, il va s'agir de la feuille contenant le hachage du cinquième bloc de donnée : Hash5. La feuille va donc être copiée de manière à faire apparaître une sixième feuille contenant également Hash5. Il n'y a plus de problème au niveau des feuilles de l'arbre puisqu'il y en a désormais une quantité paire. Cependant, nous allons rencontrer un problème au niveau supérieur. En effet, nos six feuilles vont se transformer en trois nœuds et on retombe encore une fois sur une quantité impaire. On va donc ré-itérer le procédé et dupliquer cette fois le troisième nœud contenant Hash55 (On remarque que ce hachage est obtenu en appliquant la fonction de hachage sur la concaténation de deux hachages identiques.). Cela nous permet de faire un quatrième nœud, le nombre de nœuds du niveau étant paire, on peut passer au niveau suivant. Pour l'avant |
Pour cette première approche, on va dupliquer les nœuds qui se retrouvent tout seul. Sur la '''figure 3''', on peut observer que l'arbre de Merkle contient cinq feuilles. Cinq étant un chiffre impair, notre arbre de Merkle se retrouve déséquilibré. On va donc choisir de dupliquer la feuille se retrouvant toute seule pour ré-équilibrer l'arbre. Ici, il va s'agir de la feuille contenant le hachage du cinquième bloc de donnée : Hash5. La feuille va donc être copiée de manière à faire apparaître une sixième feuille contenant également Hash5. Il n'y a plus de problème au niveau des feuilles de l'arbre puisqu'il y en a désormais une quantité paire. Cependant, nous allons rencontrer un problème au niveau supérieur. En effet, nos six feuilles vont se transformer en trois nœuds et on retombe encore une fois sur une quantité impaire. On va donc ré-itérer le procédé et dupliquer cette fois le troisième nœud contenant Hash55 (On remarque que ce hachage est obtenu en appliquant la fonction de hachage sur la concaténation de deux hachages identiques.). Cela nous permet de faire un quatrième nœud, le nombre de nœuds du niveau étant paire, on peut passer au niveau suivant. Pour l'avant-dernier niveau, on va avoir deux fois moins de nœuds que le niveau précédent, ce qui nous ramène à deux nœuds. Comme la quantité de nœuds est paire, pas besoin de dupliquer de nœud. L'algorithme de duplication prend fin ici puisque le prochain niveau va simplement contenir la racine. |
||
Notre arbre de Merkle est donc désormais équilibré et exploitable. On pourrait cependant se poser des questions sur la fiabilité de cette solution de duplication. En effet, celle-ci est assez simple à mettre en place, mais il introduit une faille de sécurité notable car certains nœuds ne contiendront en réalité qu'un seul hachage. (copié deux fois) |
Notre arbre de Merkle est donc désormais équilibré et exploitable. On pourrait cependant se poser des questions sur la fiabilité de cette solution de duplication. En effet, celle-ci est assez simple à mettre en place, mais il introduit une faille de sécurité notable, car certains nœuds ne contiendront en réalité qu'un seul hachage. (copié deux fois) |
||
==== Création d'un arbre parfait (Monero) ==== |
==== Création d'un arbre parfait (Monero) ==== |
||
| Line 91: | Line 91: | ||
[[File:Merkle_Tree_Perfect_Tree.png|thumb|right|'''Figure 4 :''' Équilibrage d'un arbre de Merkle en utilisant la technique de création d'arbre parfait (source: Medium)]] |
[[File:Merkle_Tree_Perfect_Tree.png|thumb|right|'''Figure 4 :''' Équilibrage d'un arbre de Merkle en utilisant la technique de création d'arbre parfait (source: Medium)]] |
||
Cette seconde méthode va consister à transformer n'importe quel arbre déséquilibré en un arbre parfait dès la première itération. En d'autres termes, |
Cette seconde méthode va consister à transformer n'importe quel arbre déséquilibré en un arbre parfait dès la première itération. En d'autres termes, quel que soit le nombre de blocs de données en entrée, on aura un arbre équilibré dès le premier niveau de branches (juste au dessus des feuilles). La différence avec la précédente approche où l'on dupliquait les nœuds impairs et les fusionnait avec eux-mêmes est notable puisqu'ici, on ne va pas avoir à vérifier la parité du nombre de nœuds à chaque niveau, mais seulement au tout début. L'idée va donc être de pré-calculer le nombre de transformations nécessaires sur les feuilles pour que l'on obtienne une quantité de nœuds au niveau suivant les feuilles qui soit une puissance de deux. |
||
| Line 101: | Line 101: | ||
Pour nous aider à visualiser le fonctionnement de cette approche, nous allons travailler avec l'exemple de la '''figure 4'''. Au premier coup d'œil on remarque que l'arbre a une structure un peu bizarre; on a deux niveaux de feuilles. |
Pour nous aider à visualiser le fonctionnement de cette approche, nous allons travailler avec l'exemple de la '''figure 4'''. Au premier coup d'œil on remarque que l'arbre a une structure un peu bizarre; on a deux niveaux de feuilles. Exécutons l'algorithme sans attendre pour comprendre ce qu'il se passe : |
||
* On dispose de cinq blocs de données (Data1 jusqu'à Data5). Si on cherche ''x'' tel que ''2^x > 5'', on trouve ''2^3 = 8 > 4'', soit ''x = 3''. |
* On dispose de cinq blocs de données (Data1 jusqu'à Data5). Si on cherche ''x'' tel que ''2^x > 5'', on trouve ''2^3 = 8 > 4'', soit ''x = 3''. |
||
* On soustrait désormais le nombre de blocs à la puissance trouvée, soit ''8 - 5 = 3'', ce qui nous donne l'indice de départ pour la première itération. On |
* On soustrait désormais le nombre de blocs à la puissance trouvée, soit ''8 - 5 = 3'', ce qui nous donne l'indice de départ pour la première itération. On commençant à compter les indices à partir de zéro, l'indice 3 va correspondre à Data4. Tous les blocs qui suivent Data4, lui y compris vont participer à la première itération. Tandis que tous ceux qui le précèdent vont attendre l'itération d'après. |
||
* On lance la première itération qui ne concerne ici que Data4 et Data5. On va donc naturellement calculer leur hachage respectif, ce qui nous donne Hash4 et Hash5, que l'on va concaténer et hacher de manière à obtenir Hash45, qui lui, appartient à la seconde itération. La première itération est désormais terminée puisque Data5 était le dernier nœud. |
* On lance la première itération qui ne concerne ici que Data4 et Data5. On va donc naturellement calculer leur hachage respectif, ce qui nous donne Hash4 et Hash5, que l'on va concaténer et hacher de manière à obtenir Hash45, qui lui, appartient à la seconde itération. La première itération est désormais terminée puisque Data5 était le dernier nœud. |
||
* On commence la seconde itération, avec cette fois non pas cinq nœuds mais quatre: Hash1, Hash2, Hash3 et le hachage Hash45 obtenu lors de l'itération précédente. Comme le nombre de nœuds est une puissance de deux, rien de plus simple, on va concaténer Hash1 et Hash2 pour obtenir Hash12, et Hash3 et Hash45 pour obtenir Hash345. La |
* On commence la seconde itération, avec cette fois non pas cinq nœuds, mais quatre : Hash1, Hash2, Hash3 et le hachage Hash45 obtenu lors de l'itération précédente. Comme le nombre de nœuds est une puissance de deux, rien de plus simple, on va concaténer Hash1 et Hash2 pour obtenir Hash12, et Hash3 et Hash45 pour obtenir Hash345. La seconde itération se termine. La dernière itération va concaténer Hash12 et Hash345, ce qui va nous permettre d'obtenir Hash12345. |
||
=== Validation de données === |
=== Validation de données === |
||
Revision as of 10:20, 13 December 2021
Présenté par :
- Corentin Humbert : corentin.humbert@etu.univ-grenoble-alpes.fr
- Kévin Yung : kevin.yung@etu.univ-grenoble-alpes.fr
Merkle Trees
Résumé
Les arbres de Merkle sont des arbres binaires utilisés pour effectuer de la validation de données. Pour ce faire, chaque feuille de l'arbre va contenir le hachage correspondant à une partie de la donnée à valider. Chaque nœud de l'arbre va également contenir un hachage. Ce hachage est obtenu en concaténant le hachage des deux enfants et en passant le résultat dans une fonction pour créer un tout nouveau hachage. Il se construit alors une dépendance générale où la valeur de chaque nœud dépend des valeurs de ses nœuds enfants. Chaque arbre est unique et une donnée donnera toujours le même arbre. On retrouvera typiquement les arbres de Merkle lorsqu'on voudra faire du téléchargement de fichiers sur un réseau pair-à-pair. Comme on ne peut pas vérifier l'identité des machines participant à l'envoi de fichier, il est indispensable de mettre en place une structure de vérification comme les arbres de Merkle pour s'assurer que les données reçues correspondent bien à celles désirées.
Mots-clé : arbres de Merkle, arbres binaires, hachage, structure de données, validation, pair à pair
Abstract
Merkle trees are binary trees used in data validation. A tree consists of nodes and leaves. The leaves contain the cryptographic hash corresponding to a part of the data we want to validate. The nodes contain a hash obtained by concatenating the hashes of the two child nodes and passing the concatenated string through a hashing function. This overall process creates a dependance between the nodes where each node's hash depends on the hash values of the underlying nodes. Each Merkle tree is unique and specific data will always give the same tree. A common use for Merkle trees is the download of files in peer-to-peer networks. As it is impossible to verify the identity of machines in the network, it is necessary to use validation structures such as Merkle trees to ensure that the received data is the desired one.
Keywords: Merkle trees, binary trees, hash, data structure, validation, peer to peer
Fonctionnement
Principe
Imaginons que nous voulions télécharger un fichier dans un réseau pair-à-pair, comme on ne peut pas vérifier l'identité des machines sur le réseau, il est fort probable que certaines d'entre elles tentent d'envoyer des fichiers malveillants. Il faudrait donc mettre en place un mécanisme permettant d'identifier ces fichiers non désirés. Les arbres de Merkle sont une solution à ce problème. Un arbre de Merkle est un arbre binaire qui va permettre d'identifier de manière unique et sûre une ressource sur un réseau.
Une fois qu'une donnée aura été mise en ligne sur un réseau pair-à-pair, on va la découper en plusieurs blocs et calculer les hachages pour chacun des blocs. Ces hachages de premier niveau vont constituer les feuilles de l'arbre de Merkle. Les feuilles vont ensuite être fusionnées deux à deux pour former un parent commun avec un hachage différent, et ce même parent va fusionner avec son voisin de la même manière et réitérer le processus jusqu'à obtenir la racine de l'arbre contenant le hachage unique qui va permettre d'identifier la donnée dans son intégrité.
La racine de l'arbre servant d'identifiant pour la donnée va être une manière fiable et rapide de rechercher la donnée sur le réseau. La racine va également servir à vérifier que la donnée téléchargée correspondant bien à la donnée désirée. Cela solutionne le problème initial puisque même si nous ne pouvons pas vérifier l'identité des machines, nous sommes en mesure de déterminer si la donnée reçue correspond bien à celle voulue.
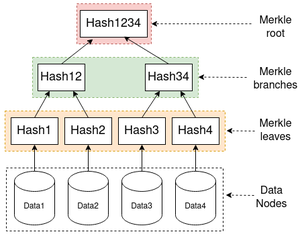
L'image ci-contre (figure 1) contient l'arbre de Merkle d'une donnée découpée en quatre blocs (Data Nodes). Juste au-dessus des blocs, on retrouve les feuilles de l'arbre (Merkle leaves) contenant les hachages des blocs. Encore au-dessus, on va retrouver les nœuds intermédiaires (Merkle branches) qui correspondent à la fusion des deux hachages du niveau précédent. Enfin, tout en haut, on retrouve la racine de l'arbre (Merkle root) qui contient le hachage final servant à identifier la donnée.
Dans la suite de ce document, nous allons présenter plus en détails les arbres de Merkle et expliquer leur fonctionnement ainsi que leurs domaines d'applications. Nous commencerons par introduire les fonctions de hachage et par décrire leur fonctionnement général ainsi que leurs avantages et désavantages. Ensuite, nous expliquerons le processus de construction d'un arbre de Merkle et tous les différents scénarios qui peuvent altérer la façon dont l'arbre va être construit. Nous enchaînerons ensuite sur la partie validation avec un exemple concret. Enfin, nous parlerons de différentes implémentations des arbres de Merkle dans des infrastructures réelles telles que la sécurité des transactions des cryptomonnaies.
Commençons sans plus attendre par faire un point sur le hachage !
Un point sur le hachage
Avant de s'immiscer dans le fonctionnement des arbres, il est important de parler du hachage et plus particulièrement des fonctions de hachage.
En cryptographie, une fonction de hachage est une fonction qui, à partir d'une donnée fournie en entrée, va être capable de calculer une empreinte numérique permettant d'identifier la donnée initiale de manière unique. La taille en sortie de cette empreinte est fixe et ne dépend pas de la taille de la donnée en entrée. Par idempotence, chaque donnée donnera toujours la même empreinte. En pratique, les fonctions de hachages sont bijectives, dans le sens où chaque donnée a une seule empreinte et chaque empreinte ne correspond qu'à une seule donnée. En théorie, la possibilité de surjectivité existe. Cela est due au fait que l'ensemble d'arrivée correspondant aux empreintes est de taille fini contrairement à l'ensemble des données en entrées qui lui peut être infini. On pourrait donc trouver deux données différentes partageant une même empreinte. Cependant, l'ensemble d'arrivée est en général suffisamment grand pour que ce phénomène ne se produise jamais. On parle souvent de la capacité qu'a une fonction de hachage à résister aux collisions (deux données différentes partageant une même empreinte). Cette capacité à résister aux collisions varie en fonction des algorithmes. Certains algorithmes réduisent d'ailleurs l'ensemble d'entrée en un ensemble fini pour s'assurer que le phénomène de collision ne se produise jamais. La présence de collisions constitue cependant une faille de sécurité importante pour les fonctions de hachages et un problème qu'on ne peut pas ignorer.
Difficilement réversible
Ce qui fait la puissance et la fiabilité d'une fonction de hachage, c'est la difficulté de retrouver la donnée initiale à partir de son empreinte. Il est très simple, pour une donnée en entrée, de calculer le hachage correspondant. Alors que l'opération inverse, qui correspond à retrouver la donnée initiale à partir de l'empreinte est mathématiquement extrêmement compliquée, et impossible à mettre en place sur les ordinateurs de nos jours. Une utilisation notable du hachage va être le stockage de mots de passe. Lors d'une inscription sur un site web, on ne va jamais stocker le mot de passe en clair dans une base de données. À la place, on va calculer le hachage correspondant au mot de passe et le stocker dans la base. À chaque fois que l'on voudra s'authentifier sur le site en rentrant le mot de passe, le hachage sera calculé et comparé à celui présent dans la base de données. Si les deux sont égaux, alors il s'agit du bon mot de passe. On peut donc vérifier qu'un mot de passe est valide sans l'avoir stocké dans la base au préalable, ce qui sécurise davantage les comptes utilisateurs.
Résistance aux collisions
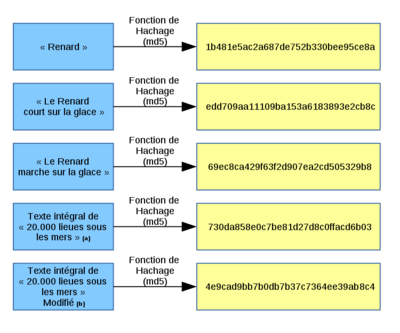
Les fonctions de hachage ont tout de même quelques faiblesses notables. La première, réside dans la complexité de l'algorithme de hachage et de sa résistance aux collisions. C'est le cas de la fonction MD5 inventée en 1991 par Ronald Rivest, qui a pu être utilisée de manière fiable jusqu'en 2004 où une équipe chinoise a réussi à casser la fonction et prouver qu'elle ne garantissait une assez bonne résistance aux collisions. Le MD5 est aujourd'hui encore utilisé dans certains cas de figure. (notamment pour vérifier l'intégrité d'une donnée, c'est le cas pour les sommes de contrôle de certaines distributions Linux par exemple.) Toutefois, il est à bannir pour le hachage de mots de passe qui sont des données extrêmement sensibles. Il existe aujourd'hui des fonctions de hachage sécurisées telles que les fonctions dites SHA (pour Secure Hashing Algorithm) et plus précisément les familles de fonctions SHA-2 et SHA-3 qui n'ont pas encore été cassées.
Limites du hachage
Une autre faiblesse des fonctions de hachage est l'idempotence. Puisque chaque donnée a une empreinte unique, un attaquant pourrait calculer en amont les hachages pour des centaines de millions de données différentes et se contenter de les comparer à des hachages volés dans des bases de données de manière à identifier la donnée source. Dans le cadre du vol de mot de passe, on parle de rainbow table qui sont simplement des gigantesques tables faisant correspondre un mot de passe à son hachage. Il existe différentes méthodes que l'on peut mettre en place pour limiter le vol de mots de passe tel que le principe de salage ou encore l'utilisation d'algorithmes lents, comme bcrypt visant à ralentir l'opération de hachage.
Enfin, il est important de garder à l'esprit que toutes les méthodes mises en place ne résolvent pas le problème, elles visent simplement à ralentir considérablement les attaquants. Un attaquant disposant de suffisamment de temps et de puissance de calcul finira par retrouver n'importe quel mot de passe. Il y a également les récentes innovations au niveau des ordinateurs quantiques qui sont vouées à compromettre significativement les dispositifs de sécurité mis en place sur Internet aujourd'hui. Nous ne nous étendrons pas plus sur le sujet du hachage dans ce document, si vous désirez en apprendre davantage, je vous invite à cliquer sur les différents liens hypertextes présents dans cette partie.
Création d'un arbre
Pour réaliser un arbre de Merkle pour une donnée particulière, on va commencer par découper la donnée en entrée en un certain nombres de blocs. Le nombre de blocs va varier en fonction de la taille de la donnée. Une fois la donnée scindée en blocs, on va calculer pour chaque bloc son hachage et l'ajouter à l'arbre de Merkle. Deux blocs consécutifs vont être reliés par un nouveau nœud parent dont le hachage sera calculé en effectuant la concaténation des deux hachages enfant et en hachant une dernière fois ce résultat. On va réitérer cette opération pour chaque bloc, jusqu'à ce que tous les blocs de données hachés appartiennent à l'arbre et qu'une racine soit calculée. Une fois la racine obtenue, la construction de l'arbre est terminée.
Pour ce qui est de l'algorithme de hachage utilisé, celui-ci va varier en fonction des implémentations. Généralement, on utilisera des fonctions de hachage robustes tel que le SHA2 ou SHA3.
Arbre de Merkle déséquilibré
Nous avons parlé précédemment de comment les arbres de Merkel étaient construits, mais nous avons oublié d'évoquer un point. L'algorithme décrit marche très bien lorsque le nombre de blocs en entrée est une puissance de 2. Par exemple, avec quatre blocs, on aura quatre feuilles (nœud de hauteur 2), deux nœuds de hauteur 1 et un nœud de hauteur 0 (la racine). Mais que se passe-t-il si au lieu d'avoir quatre blocs, nous en avions six ? Nous aurions alors six feuilles, trois nœuds de hauteur 1 et... Comment faire ? Chaque nœud ne peut avoir que deux enfants et nous nous trouvons avec un nombre impair de nœud, devons-nous changer la structure de l'arbre et autoriser des nœuds à avoir trois enfants ?
Ils existent différentes approches permettant de pallier ce problème.
Duplication du nœud impair (Bitcoin)
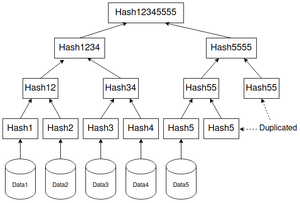
Pour cette première approche, on va dupliquer les nœuds qui se retrouvent tout seul. Sur la figure 3, on peut observer que l'arbre de Merkle contient cinq feuilles. Cinq étant un chiffre impair, notre arbre de Merkle se retrouve déséquilibré. On va donc choisir de dupliquer la feuille se retrouvant toute seule pour ré-équilibrer l'arbre. Ici, il va s'agir de la feuille contenant le hachage du cinquième bloc de donnée : Hash5. La feuille va donc être copiée de manière à faire apparaître une sixième feuille contenant également Hash5. Il n'y a plus de problème au niveau des feuilles de l'arbre puisqu'il y en a désormais une quantité paire. Cependant, nous allons rencontrer un problème au niveau supérieur. En effet, nos six feuilles vont se transformer en trois nœuds et on retombe encore une fois sur une quantité impaire. On va donc ré-itérer le procédé et dupliquer cette fois le troisième nœud contenant Hash55 (On remarque que ce hachage est obtenu en appliquant la fonction de hachage sur la concaténation de deux hachages identiques.). Cela nous permet de faire un quatrième nœud, le nombre de nœuds du niveau étant paire, on peut passer au niveau suivant. Pour l'avant-dernier niveau, on va avoir deux fois moins de nœuds que le niveau précédent, ce qui nous ramène à deux nœuds. Comme la quantité de nœuds est paire, pas besoin de dupliquer de nœud. L'algorithme de duplication prend fin ici puisque le prochain niveau va simplement contenir la racine.
Notre arbre de Merkle est donc désormais équilibré et exploitable. On pourrait cependant se poser des questions sur la fiabilité de cette solution de duplication. En effet, celle-ci est assez simple à mettre en place, mais il introduit une faille de sécurité notable, car certains nœuds ne contiendront en réalité qu'un seul hachage. (copié deux fois)
Création d'un arbre parfait (Monero)
Cette seconde méthode va consister à transformer n'importe quel arbre déséquilibré en un arbre parfait dès la première itération. En d'autres termes, quel que soit le nombre de blocs de données en entrée, on aura un arbre équilibré dès le premier niveau de branches (juste au dessus des feuilles). La différence avec la précédente approche où l'on dupliquait les nœuds impairs et les fusionnait avec eux-mêmes est notable puisqu'ici, on ne va pas avoir à vérifier la parité du nombre de nœuds à chaque niveau, mais seulement au tout début. L'idée va donc être de pré-calculer le nombre de transformations nécessaires sur les feuilles pour que l'on obtienne une quantité de nœuds au niveau suivant les feuilles qui soit une puissance de deux.
L'algorithme utilisé est le suivant :
- On commence par trouver x, tel que 2^x soit supérieur au nombre de blocs de données. (cela revient à utiliser un logarithme en base 2)
- On soustrait ensuite à 2^x le nombre de blocs de données, cela va nous donner l'indice auquel nous allons commencer la première itération de construction de l'arbre
- On procède en effectuant la première itération à partir du bloc de donnée correspondant à l'indice trouvé.
- Une fois la première itération terminée, le nombre de nœuds à l'itération suivante est une puissance de deux, on peut procéder normalement sans avoir à se soucier de potentiels problème de parité.
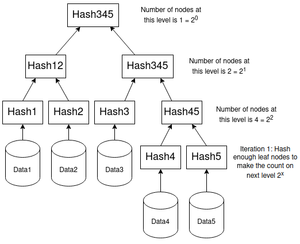
Pour nous aider à visualiser le fonctionnement de cette approche, nous allons travailler avec l'exemple de la figure 4. Au premier coup d'œil on remarque que l'arbre a une structure un peu bizarre; on a deux niveaux de feuilles. Exécutons l'algorithme sans attendre pour comprendre ce qu'il se passe :
- On dispose de cinq blocs de données (Data1 jusqu'à Data5). Si on cherche x tel que 2^x > 5, on trouve 2^3 = 8 > 4, soit x = 3.
- On soustrait désormais le nombre de blocs à la puissance trouvée, soit 8 - 5 = 3, ce qui nous donne l'indice de départ pour la première itération. On commençant à compter les indices à partir de zéro, l'indice 3 va correspondre à Data4. Tous les blocs qui suivent Data4, lui y compris vont participer à la première itération. Tandis que tous ceux qui le précèdent vont attendre l'itération d'après.
- On lance la première itération qui ne concerne ici que Data4 et Data5. On va donc naturellement calculer leur hachage respectif, ce qui nous donne Hash4 et Hash5, que l'on va concaténer et hacher de manière à obtenir Hash45, qui lui, appartient à la seconde itération. La première itération est désormais terminée puisque Data5 était le dernier nœud.
- On commence la seconde itération, avec cette fois non pas cinq nœuds, mais quatre : Hash1, Hash2, Hash3 et le hachage Hash45 obtenu lors de l'itération précédente. Comme le nombre de nœuds est une puissance de deux, rien de plus simple, on va concaténer Hash1 et Hash2 pour obtenir Hash12, et Hash3 et Hash45 pour obtenir Hash345. La seconde itération se termine. La dernière itération va concaténer Hash12 et Hash345, ce qui va nous permettre d'obtenir Hash12345.
Validation de données
Dans les parties précédentes, nous avons vu ce qu'étaient les arbres de Merkle, et comment procéder pour en construire un. Toutefois, nous n'avons pas encore vu comment les uiliser. Nous avons parlé brièvement du fait qu'ils servaient à faire de la validation de données mais nous n'avons pas encore détaillé exactement comment. C'est ce dont nous allons parler dans cette partie.
Imaginons que nous voulions télécharger un fichier assez conséquent depuis Internet. On veut utiliser un système pair à pair pour télécharger le fichier. On ne va donc pas se connecter à un serveur unique qui détient le fichier désiré mais à une multitude de machines dans un réseau qui vont participer au téléchargement. Le pair à pair a de nombreux avantages mais nous ne rentrerons pas en détail sur son fonctionnement dans ce document. L'un des problèmes majeurs des architectures pair à pair est la confiance que l'on accorde à chaque machine. En effet, contrairement à une architecture client-serveur classique où le serveur est une machine identifiée et à laquelle on fait généralement confiance, la modularité des systèmes pair à pair fait que nous soyions obligé de nous reposer sur des machines anonymes et potentiellement malicieuses. Il est impossible de vérifier si chaque machine est légitime ou si l'une d'entre elles tente de nous envoyer un fichier corrompu. C'est justement pour pallier ce problème que nous pouvons utiliser les arbres de Merkle.
Reprenons notre problèmatique de téléchargement de fichier. Ici, le fichier que l'on veut obtenir va être transformé en un arbre de Merkle. En d'autres termes, il va être divisé en un certain nombre de blocs que l'on va hacher un à un jusqu'à obtenir un hachage unique qui permet d'identifier l'intégralité du fichier (il s'agit de la racine de l'arbre). Nous avons donc un arbre plus ou moins massifs qui va représenter le fichier que nous voulons télécharger. Mais comment-va-t'on faire pour vérifier que le fichier que nous avons demandé est bien celui que nous avons reçu ? Tout repose sur le hachage racine. Si on part du principe que nous avons obtenu le hachage racine d'un tier auquel nous faisons confiance, nous allons pouvoir, par ce seul hachage, s'assurer que le fichier que nous obtenons soit bel et bien celui que nous voulions.
Prenons un exemple très simple: On veut télécharger un fichier F en utilisant un réseau pair à pair. On dispose du hachage unique permettant d'identifier le fichier grâce à un tier à qui nous faisons confiance. Ce hachage, un peu à la manière d'un URL va permettre d'identifier le fichier au sein du réseau. On va donc indiquer le fichier que l'on désire télécharger en fournissant son hachage et les pairs vont s'occuper de nous envoyer les blocs de données. A ce niveau-là, nous ne pouvons rien dire sur la légitimité des machines qui nous envoient les blocs de données, il est possible que certaines d'entres elles soient malicieuses mais impossible pour nous de vérifier. Toutefois, lorsque nous aurons reçu tous les blocs de données, nous allons pouvoir les valider en reconstruisant l'arbre de Merkle et en vérifiant que le hachage racine obtenu est identique à celui que nous avions à l'origine. S'il s'agit du même hachage, alors le fichier est bien conforme. Si l'une des machines du réseau pair à pair a tenté de nous envoyer des données non légitimes, on va pouvoir très facilement le détecter. En effet, comme chaque noeud dépend des noeuds qui le précède, le moindre changement va se propager et changer completement le hachage racine.
L'efficacité des arbres de Merkle a détecter le moindre changement de bit dans un fichier repose sur la nature des fonctions de hachage qu'il utilise. En effet, une particularité des fonctions de hachage est qu'elles sont très chaotiques et que le changement du moindre bit va complètement changer le hachage résultant.
Cas d'utilisations
Git
Git est un logiciel de gestion de versions décentralisé qui est beaucoup utilisé aujourd'hui. Tous les fichiers sont enregistrés sur l'ordinateur de tous les utilisateurs, à tout moment. Les Merkle trees permettent d'assurer que tout changement soit cohérent sur les ordinateurs de tous les utilisateurs. En comparant simplement le hashages des fichiers ou dossiers entre 2 différents commits, on peut facilement et surtout rapidement savoir si celui-ci a été modifié ou non.
Cryptomonnaie
La cryptomonnaie a été très popularisé récemment, et continuer de s'étendre, notamment le bitcoin. Toutes les transactions de cryptomonnaie sont stockées dans des blocks, aussi appelés blockchain. La cryptomonnaie utilise les Merkle Trees pour s'assurer la validation des transactions dans les blocks. En effet, les blocks contiennent un ID, qui est le header fields hashé (cf. image), et parmi ce header hashé, une partie contient la racine de du Merkle Tree. De ce fait, elle permet de s'assurer de l'unicité de l'enregistrement des transactions dans le block.
Blockchain pruning
Pour continuer sur le sujet des cryptomonnaies, l'émondation ou l'élagage des blockchains est un sujet qui reste d'affût de nos jours. En effet, sachant que les blockchains grandissent de plus en plus actuellement, cela veut également dire que celles-ci prennent de plus en plus de place en terme de stockage. Par exemple, en Février 2021, la taille de la blockchain du Bitcoin est d'environ 380Go. De ce fait, l'élagage de la blockchain consiste à épurer l'arbre, en supprimant les informations de la blockchain non critiques de l'espace de stockage. Les noeuds pleins gardent une copie de tous ce qui est stockés dans la blockchain, notamment des informations qui ne sont plus forcément utiles. Sachant que l'objectif d'un Merkle Tree est de synthétiser et de relier de grandes quantités d'informations. Chaque noeud contient l'information de ses fils, et donc la proposition est d'élaguer les informations qui ne sont plus utiles commes les transactions utilisées, ne laissant que les branches contenant les hashages pour vérifier les autres transactions.
Base de données (AWS Dynamo DB)
Dynamo DB est une base de données distribuée provenant en partie de la plateforme Amazon Web Services. C'est une base de données key-value NoSQL, entièrement managée et serverless qui est designé pour exécuter des applications hautes performances à n'importe quelle échelle. Dynamo DB héberge les données (values) dans des data nodes qui sont aussi appelés "virtual nodes" et chaque virtual nodes héberge une key-range (gamme de clés). Un Merkle tree est construit pour chaque key-range, où les feuilles de l'arbre sont les valeurs de la key-range data. La Merkle Root contient donc un résumé des données de chaque noeuds. De ce fait, en comparant les Merkle Roots de chaque virtual nodes qui possèdent les mêmes key-range, on peut donc monitorer la moindre différences et de repérer l'endroit divergent.
File System (ZFS)
Conclusion
Les arbres de Merkle sont très pratiques pour effectuer de la validation de données dans un système pair à pair. Ils ne sont pas difficile à stocker puisque les seules données qu'ils contiennent (en dehors des blocs de données) vont être des hachages dont la taille varie autour de la centaine d'octets en fonction des algorithmes de hachage utilisés. Leur simplicité permet également une validation rapide des données puisqu'il suffit de faire des opérations de concaténation (très faible coût) et de calcul de hachage (coût faible en moyenne, peut varier suivant la fonction de hachage utilisée). La structure en arbre permet également d'apporter une certaine granularité et l'ajout de fonctionnement annexe par rapport à une simple concaténation des hachages de chaque bloc de données. Enfin, la robustesse d'un arbre va entièrement dépendre des fonctions de hachages utilisées. Par exemple, si l'on voulait valider des données sensibles comme des transactions sur la blockchain, on préferera utiliser des fonctions sécurisées comme celles de la famille SHA plutôt qu'un simple md5.
Références
- "Merkle Trees: Concepts and Use Cases", Medium, https://medium.com/coinmonks/merkle-trees-concepts-and-use-cases-5da873702318
- "Merkle tree", Wikipedia, https://en.wikipedia.org/wiki/Merkle_tree
- "Fonction de hachage", Wikipedia, https://fr.wikipedia.org/wiki/Fonction_de_hachage
- "How Merkle Trees Enable the Decentralized Web!", Youtube (Coding Tech channel), https://www.youtube.com/watch?v=YIc6MNfv5iQ