VT2015 Factoring RSA

Présentation

• Enseignants : Georges-Pierre Bonneau, Didier Donsez (VT2015)
• Sujet : Factoring RSA Keys With TLS Perfect Forward Secrecy
• Auteur : Sébastien TOUSSAINT
• Date : 02 octobre 2015

Mots Clés

RSA, théorème des restes chinois, TLS, Perfect foward secrecy, confidentialité persitante, handshake, diffie-hellman.

Abstract

The significant growth of transactions on the Internet in the early-mid 90s and early 2000s raised awareness among researchers to find and develop data security techniques on the internet. The September 21, 2000, the end RSA encryption patent previously held by the Massachusetts Institute of Technology (MIT), was a breakthrough in securing confidential data on the internet. This encryption system is the safest today. An article mad by Florian Weimer published Sept. 2, 2015 said it is possible to retrieve RSA private keys, especially if they were implemented using the Chinese remainder theorem. RSA encryption with forward secrecy TLS protocols are safe. But the implementation of these protocols can be badly performed and therefore be vulnerable to Lenstra attacks. To prevent this problem it is necessary to verify the implementation of these algorithms and ensure that it is not vulnerable to hardware problems.

Résumé

La croissance importante des transactions effectuées sur internet dans le début-milieu des années 90 et début des années 2000 a sensibilisé les chercheurs à trouver et développer des techniques de sécurisation des données sur internet. Le 21 septembre 2000, la fin du brevet de chiffrement RSA détenu jusqu’alors par le Massachusetts Institute of Technology (MIT), fut une grande avancée dans la sécurisation des données confidentielles sur internet. Ce système de chiffrement est le plus sûr aujourd’hui. Un article de Florian Weimer paru le 2 septembre 2015 dit qu’il est possible de récupérer des clés privées de RSA, spécialement si elles ont été implémentées été implémenté à l’aide du théorème des restes chinois. Le chiffrement RSA avec la confidentialité persistante de TLS sont des protocoles sûrs. Mais l’implémentation de ces protocoles peut être mal effectuée et donc être vulnérable aux attaques de Lenstra. Pour prévenir ce problème il faut bien vérifier l’implémentation de ces algorithmes et faire en sorte qu’il ne soit pas vulnérable aux problèmes matériels.

Synthèse

Introduction

La croissance importante des transactions effectuées sur internet dans le début-milieu des années 90 et début des années 2000 a sensibilisé les chercheurs à trouver et développer des techniques de sécurisation des données sur internet. Le 21 septembre 2000, la fin du brevet de chiffrement RSA détenu jusqu’alors par le Massachusetts Institute of Technology (MIT), fut une grande avancée dans la sécurisation des données confidentielles sur internet. Ce système de chiffrement est le plus sûr aujourd’hui. Un article de Florian Weimer paru le 2 septembre 2015 dit qu’il est possible de récupérer des clés privées de RSA, spécialement, si elles ont été implémentées été implémenté à l’aide du théorème des restes chinois. Nous allons dans cette synthèse revenir sur les bases de RSA, du théorème des restes chinois et le TLS perfect foward secrecy avec ses mécanismes (handshake, Diffie-Hellman) avant d’étudier les travaux de Florian Weimer.

Le chiffrement RSA

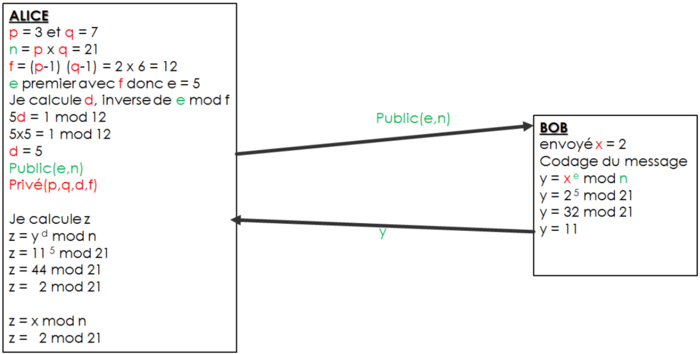
Le chiffrement RSA est un système de cryptographie asymétrique. Cela signifie qu’il y existe deux clés dans notre système. Une clé privée connue par une seule entité. Elle va lui permettre de déchiffrer les messages qui lui ont été envoyés. Une clé publique connue de tout le monde et qui va chiffrer le message que l’on souhaite envoyer. Ces clés sont produites par une seule entité.

L’image ci-dessus représente une communication RSA entre deux utilisateurs, Alice et Bob. Les éléments en vert sur l’image représentent les informations en clair dans le canal de communication de ce protocole, donc tout le monde y a accès. Les éléments en rouge représentent les informations privées de chaque utilisateur. Donc du côté d’Alice ces informations permettent de créer sa clé privée. Tout d’abord Alice choisit deux nombres premiers distincts p et q puis elle fait leur produit afin d’obtenir le nombre n, ensuite l’indicateur de Euler ou fonction Phi de n f = (p-1) (q-1). Puis on calcul e premier avec f donc e = 5 et on calcule d, inverse de e modulo f. Donc pour chiffrer les messages nous avons y = x^e mod n. Et pour déchiffrer les messages nous avons z = y^d mod n.

Le théorème des restes chinois

Théorème : Prenons m1, ..., m n des entiers supérieurs à 2 deux à deux premiers entre eux, et a1,...,an des entiers. Le système d'équations :

admet une unique solution modulo M=m1×⋯×mn qui est donnée par la formule : x=a1M1y1+⋯+anMnyn où Mi = et yi = Mod mi pour tout i compris entre 1 et n.

Transport Layer Security (TLS)

Transport Layer Security (TLS) est un protocole qui garantit la confidentialité entre les applications et leurs utilisateurs sur Internet. Quand un serveur et le client communiquent, TLS garantit qu'aucun tiers ne peut être espionné ou altérer un message. TLS est le successeur du protocole Secure Sockets Layer (SSL). Ce type de protocole est né du fait que plusieurs sites ont commencé à proposer des transactions (achats en ligne notamment). Afin de favoriser l’utilisation de ces plateformes de transaction, des protocoles de sécurisation des données des utilisateurs furent mis en place. En 2009, TLS est utilisé par la plupart des navigateurs Web. L'internaute peut reconnaître qu'une transaction est chiffrée à plusieurs signes :

• l'URL dans la barre d'adresse commence par https et non http (https://...) ;
• affichage d'une clé ou un cadenas

La confidentialité persistante (Perfect Forward Secrecy)

Une fois que la clé privée de certains sites Web HTTPS est compromise, un attaquant est capable de construire une attaque « man-in-the-middle » pour intercepter et décrypter toute communication avec le site Web. La première étape contre une telle attaque est la révocation du certificat associé. Malheureusement, l'attaquant pourrait également avoir enregistré des communications passées protégées par cette clé privée et donc les décrypter. Forward secrecy permet à l'information d'aujourd'hui d’être gardée secrète, même si la clé privée est compromise dans l'avenir. La réalisation de cette propriété est généralement coûteuse et par conséquent, la plupart des serveurs web ne le permet pas.

Diffie-Hellman & Handshake

Handshake

En informatique, en télécommunications et dans les domaines associés, le handshaking ou "handshake" ("poignée de main" en français) est un processus automatisé de négociations qui établit les paramètres d'une communication entre deux entités avant que la communication commence. Un handshake est fait au moment où un ordinateur veut entreprendre une communication avec un appareil plus ou moins éloigné, par exemple un modem, une imprimante ou un serveur.

Diffie-Hellman

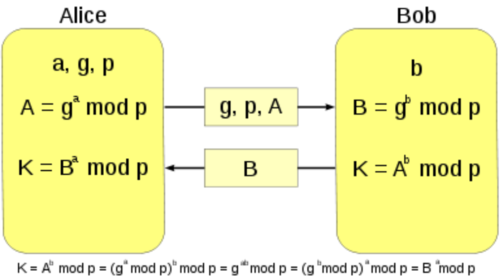
Diffie-Hellman est une méthode par laquelle deux personnes nommées conventionnellement Alice et Bob peuvent se mettre d'accord sur un nombre (qu'ils peuvent utiliser comme clé pour chiffrer la conversation suivante) sans qu'une troisième personne appelée Ève puisse découvrir le nombre, même en ayant écouté tous leurs échanges.

Factoring RSA Keys With TLS Perfect Forward Secrecy

Dans un rapport de Florian Weimer paru le 9 septembre 2015, ce dernier affirme avoir réussi à récupérer des clés RSA. En effet il dit que les protocoles utilisant le protocole RSA avec les théorèmes des restes chinois pour mettre en place le TLS avec de la confidentialité persistante sont les plus vulnérables. Mais les seuls genres d’attaques capables de permettre une telle vulnérabilité sont les attaques Lenstra.

Les attaques Lenstra sont des attaques sur les canaux auxiliaires. Ils sont dus à de mauvaises implémentations logicielles ou matérielles (veilles librairies, UAL fatiguée, erreurs dans une mémoire cache …) des crypto-systèmes. Donc cela ne remet pas en cause les protocoles de cryptographie et ici dans notre cas le RSA.

La faille

Dans le rapport de Weimer, la formule utilisée pour effectuer la signature est la suivante :

• y_p = x^d modulo p
• y_q = x^d modulo q
• y = y_p q (q^{-1} modulo p) + y_q p (p^{-1} modulo q) modulo n.

Mais si un problème survient durant le calcul de y_p, que nous allons appeler w_p. Alors nous avons

• Y = Y_p modulo p
• Y = y_q modulo q

Si nous mettons le tout à la puissance (voir rappel sur RSA) et que nous enlevons x nous avons :

• Y^e - x = Y_p^e - x = a modulo p
• Y^e - x = y_q^e - x = 0 modulo q

Et là nous savons que q divise w_p et que q divise aussi n. Alors que p ne divise plus Y^e – x. Il nous reste plus qu’à faire le PGCD de n et Y^e – x pour trouver q.

D’un point de vue réseau il s’agit d’une trame en plus que fournit le serveur au client durant le handshake TLS. Dans cette trame il y a la clé publique du serveur. Cette trame ne dit pas quel algorithme a été utilisé pour faire l’échange de clé; et ceci peut conduire à une longue série d’attaque. Selon le rapport de Florian Weimer il existe un seul moyen de prévenir cette erreur, il faut vérifier que la signature ait été bien faite.

Cette fuite est visible pour le client qui réalise la poignée de mains TLS ou un observateur passif qui intercepte le trafic réseau" écrit Florian Weimer

Florian Weimer explique que "dans les cas de fuites de clés que nous avons observé, l'attaquant à distance ne peut pas organiser une fuite de clés à la demande étant donné qu'il n'est pas en mesure de manipuler le serveur du réseau d'une manière qui augmenterait la probabilité d'une fuite de réseau dans une poignées de main TLS. L'individu malintentionné peut uniquement intercepter un maximum de poignées de main, probablement en initialisant une multitude de poignées".

A ne pas faire

"La désactivation de la confidentialité persistante permettrait aux observateurs passifs qui auraient voler des clés, de déchiffrer les sessions TLS à venir dans le trafic réseau intercepté, sans devoir rediriger la connexion du client. Autrement, la désactivation de la confidentialité persistante ne contribue qu'à la détérioration de la situation. (la désactivation de la confidentialité persistance et le remplacement du certificat du serveur, quant à eux, fonctionnent)" écrit Florian Weimer.

Conclusion

Pour résumer, le chiffrement RSA avec la confidentialité persistante de TLS sont des protocoles sûrs. Mais l’implémentation de ces protocoles peut être mal effectuée et donc être vulnérable aux attaques de Lenstra. Pour prévenir ce problème il faut bien vérifier l’implémentation de ces algorithmes et faire en sorte qu’il ne soit pas vulnérable aux problèmes matériels.

Concernant les logiciels qui utilisent ces protocoles, ils ont été prévenus et ont mieux protégés leurs implémentations. Si vous voulez savoir si votre système est bien implémenté il est conseillé de contacter votre fournisseur d'outil d'outils de chiffrement pour en être certain.

Notes et références

  - https://securityblog.redhat.com/2015/09/02/factoring-rsa-keys-with-tls-perfect-forward-secrecy/
  - http://villemin.gerard.free.fr/Crypto/RSA.htm
  - http://blog.terraverdeservices.com/rsa-key-factoring-vulnerability-using-perfect-forward-secrecy
  - https://www.nccgroup.trust/us/about-us/newsroom-and-events/blog/2015/september/factoring-rsa-keys-with-tls-perfect-forward-secrecy/
  - https://simple.wikipedia.org/wiki/Diffie-Hellman_key_exchange
  - http://bibmath.net/crypto/index.php?action=affiche&quoi=complements/resteschinois